雷射共振腔模式

雷射光束形狀是由共振腔決定， a laser optical mirror，雷射光在共振腔的增益媒介中放大。 Laser resonators are typically formed by using highly reflective dielectric mirrors or a monolithic crystal that utilizes total internal reflection to keep light from escaping (Figure 1). Below is a list of common laser resonator geometries¹:

Plane parallel resonator: two flat mirrors separated by a distance equal to an integral multiple of one half of the lasing wavelength
Concentric resonator: two spherical mirrors with the same radius of curvature and coincident centers of curvature
Confocal resonator: two spherical mirrors with the same radius of curvature and coincident focal points
Ring resonator: ring of more than two reflectors where the total closed loop path of the reflected light is equal to an integral multiple of one half of the lasing wavelength

Figure 1: Four common types of laser resonator geometries where n is an integer value, λ is the lasing wavelength, R is the radius of curvature of a curved mirror, and f is the focal length of a curved mirror

Resonator cavities are “stable” if the reflected light stays inside the cavity, even as the number of reflections approaches infinity (Figure 2). In this instance, the only way for light to leave the cavity is through a partially reflective mirror. On the other hand, resonator cavities are considered “unstable” if the reflected light continuously diverges as the number of reflections approaches infinity. When this occurs, the beam size will grow until it is larger than the reflectors and then escape the system. Stable resonators are often used with lasers that have powers up to 2kW to achieve high gain and improve directionality. Unstable resonators are typically used with higher power lasers to reduce the chance of damaging the reflectors.¹

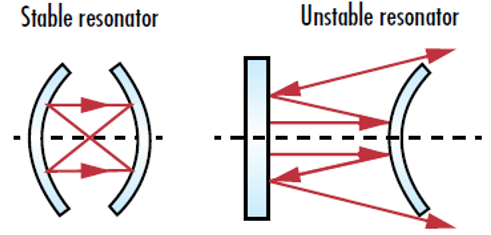
Figure 2: Stable laser resonators keep all reflected beams inside the confines of the cavity, while unstable resonators cause reflected light to spread out until it eventually escapes the cavity

共振腔路徑長度決定縱向共振腔模式，或是電場分布；電場分布會在共振腔內造成駐波。光束模式決定其形狀。這些模式維持其振幅剖面，並在共振腔內完成一個封閉迴路後自行複製（除了可能因為共振腔損耗而喪失部分功率）。為了產生共振模式，也必須在單一封閉迴路路徑產生相當於 2π 整數倍數的相位偏移 (圖 3).

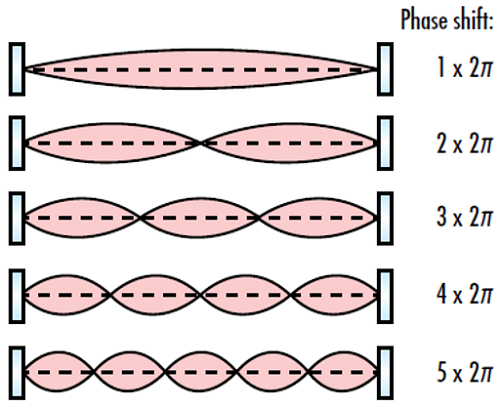
Figure 3: The phase shift of a complete loop in an optical resonator must be an integer multiple of 2π in order for a resonant mode to occur

圖 3: 光學共振腔中完整迴路的相位偏移，必須為 2π 的整數倍數，以便產生共振模式

最簡單的雷射共振腔模式類型為厄米特高斯 (Hermite-Gaussian) 模式，也稱為橫向電磁模式 (TEM_nm)；其中可利用高斯函數與厄米特多項式的乘積估計電場剖面1:²:

\begin{align}
E_{nm} \! \left(x, y, z \right) = & \, E_0 \frac{w_0}{w \! \left( z \right)} \, \cdot \, H_{n} \left( \sqrt{2} \frac{x}{w \! \left( z \right)} \right) \\
& \cdot \exp{\left( -\frac{x^2}{w \! \left( z \right) ^2} \right)} \, \cdot \, H_m \left( \sqrt{2} \frac{y}{w \! \left( z \right)} \right) \cdot \exp{\left( -\frac{y^2}{w \! \left( z \right) ^2} \right)} \\
& \cdot \, \exp{\Bigg[ -i \left[ kz - \left( 1 + n + m \right) \cdot \tan^{-1}{\left( \frac{z}{z_R} \right)} + \frac{k \left( x^2 + y^2 \right)}{2 R \! \left( z \right) } \right] \Bigg]}
\end{align}

\begin{align} E_{nm} \! \left(x, y, z \right) = & \, E_0 \frac{w_0}{w \! \left( z \right)} \, \cdot \, H_{n} \left( \sqrt{2} \frac{x}{w \! \left( z \right)} \right) \\ & \cdot \exp{\left( -\frac{x^2}{w \! \left( z \right) ^2} \right)} \, \cdot \, H_m \left( \sqrt{2} \frac{y}{w \! \left( z \right)} \right) \cdot \exp{\left( -\frac{y^2}{w \! \left( z \right) ^2} \right)} \\ & \cdot \, \exp{\Bigg[ -i \left[ kz - \left( 1 + n + m \right) \cdot \tan^{-1}{\left( \frac{z}{z_R} \right)} + \frac{k \left( x^2 + y^2 \right)}{2 R \! \left( z \right) } \right] \Bigg]} \end{align}

\begin{align} E_{nm} \! \left(x, y, z \right) = & \, E_0 \cdot H_n \cdot H_m \frac{w_0 \, x \, y}{\left[ w \! \left( z \right) \right]^3} \cdot \exp{\left[ - \left( \frac{x}{w \! \left( z \right)} \right)^2 \right]} \cdot \exp{\left[ - \left( \frac{y}{w \! \left( z \right)} \right)^2 \right]} \\ & \cdot \exp{\Bigg[ -i \left[ kz - \left( 1 + n + m \right) \cdot \tan^{-1}{\left( \frac{z}{z_R} \right)} + \frac{k \left( x^2 + y^2 \right) }{2 R \! \left( z \right)} \right] \Bigg]} \end{align}

E₀ 為場最大值
x 及 y 為定義光束截面的軸
z 為傳播軸
w₀ 為束腰
w(z) 為特定 z 值情況下的光束半徑
H_n(x) 及 H_m(x) 為厄米特多項式，其中具有非負數整數的指數 n 及 m
k 為波數 (k=2π/λ)
z_R 為雷利範圍
R(z) 為波前曲率半徑

整數 n 及 m 分別定義 x 及 y 方向的光束形狀。理想的高斯光束是由模式 TEM₀₀, 定義，於 n 及 m 均等於 0 時產生 (圖 4)。如需更多資訊瞭解高斯光束，請參閱高斯光束傳播。所有其他的 n 及 m 值，都會產生更複雜的共振腔模式。³ 圖 5, 顯示最低階厄米特高斯模式的截面幾何，其中 n 及 m 值介於 0 至 3 之間。

圖 4: 厄米特高斯共振腔模式 TEM₀₀ 對應於完美高斯光束

Figure 5: Cross-sections of the lowest-order Hermite-Gaussian resonator modes with n and m values ranging from 0 to 3

圖 5: 最低階厄米特高斯模式的截面，其中 n 及 m 值介於 0 至 3之間

參考資料

“Section 2.6: Various Laser Resonators.” Advanced Manufacturing Laboratory, Columbia Engineering, www.aml.engineering.columbia.edu/ntm/level2/ch02/html/l2c02s06.html.
Paschotta, Rüdiger. Encyclopedia of Laser Physics and Technology, RP Photonics, October 2017, www.rp-photonics.com/encyclopedia.html.
Paschotta Rüdiger. Field Guide to Lasers. SPIE Press, 2008.

上個章節下個章節 Next Section

更多技術資源