色散

色散是光在穿透光學介質時，其相位速度或相位延遲與其他參數之間的相依性，例如光學頻率或波長。雷射光學基底: 內部可能發生多種不同類型的色散，例如色度 (圖 1), intermodal, and polarization mode dispersion.¹

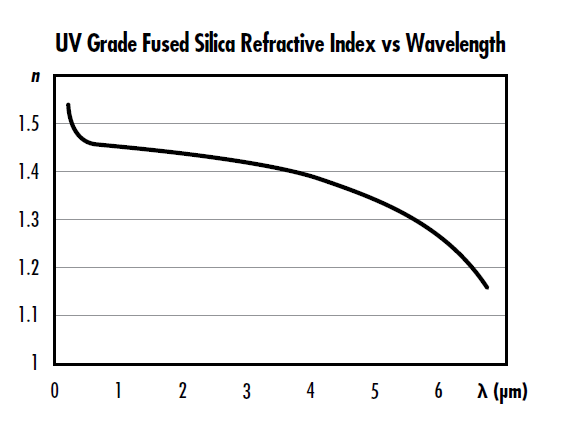
$>Figure 1: Refractive index of UV Grade fused silica as a function of wavelength$

圖 1: 紫外線級熔融石英折射指數作為波長函數

色度色散

折射指數是指真空中的光速，與穿透介質（例如空氣或玻璃）時光波相位速度之間的比率。脈衝雷射應用普遍以頻率描述光線，因為一般而言時間更為關鍵，而光線頻率為固定值，且其波長需視其穿越環境內部的折射指數而定。波長 $ \small{\left( \lambda \right)} $ 與角頻率 $ \small{\left( \omega \right)} $, 折射指數 $ \small{\left( n \right)} $, 及光速 $ \small{\left( c \right)} $ 有關:

(1)$$ \lambda = \frac{2 \pi \, c}{\omega \, n} $$

材料折射指數通常以 Selmeier 公式及材料常數 $\small{B_1}$, $\small{B_2}$, $\small{B_3}$, $\small{C_1}$, $\small{C_2}$, and $\small{C_3}$:

(2)$$ n^2 \! \left( \lambda \right) - 1 = \frac{B_1 \, \lambda ^2}{\lambda ^2 - C_1 } + \frac{B_2 \lambda^2}{\lambda^2 - C_2} + \frac{B_3 \lambda^2}{\lambda ^2 -C_3} $$

色度色散為光線在介質中的相位速度 $\small{\nu _{p}}$ ，與光線波長之間的相依性，大多是由光線與介質電子之間的互動所產生。色度色散是以阿貝數 (圖 2), 描述，對應於與 $ \small{\lambda} $, 相關折射指數第一偏導數的倒數，而部分色散則對應於與波長相關折射指數的第二導數。

圖 2: 阿貝圖顯示一般玻璃類型折射指數與其阿貝數的比較情形。CTE（熱膨脹係數）於光學基板的熱性能

阿貝數公式如下:

(3)$$ V_D = \frac{n_D - 1}{n_F - n_C} $$

$\small{n_D} $, $\small{n_F} $, 及 $\small{n_C} $ 為基材 Fraunhofer D- $ \small{\left( 589.3 \text{nm} \right)} $, F- $ \small{\left( 486.1 \text{nm} \right)} $, 及 C- $ \small{\left( 656.3 \text{nm} \right)} $ 光譜線波長情況下的折射指數。材料阿貝數也可利用與波長相關的折射指數導數，於任何波長描述:

(4)$$ V _{\lambda} = -\frac{1}{2} \left(n - 1 \right) \frac{\text{d} n}{\text{d} \lambda} $$

In laser applications, the primary concern is how dispersion will affect the properties of a laser pulse traveling through the medium, which is described by group velocity - the variation of the phase velocity of light in a medium relative to its wavenumber:

(5)$$ \nu _g = \left( \frac{\partial k}{\partial \omega} \right)^{-1} = c \left[ \frac{\partial}{\partial \omega} \left( \omega n \! \left( \omega \right) \right) \right] ^{-1} = \frac{c}{n \! \left( \omega \right) + \omega \frac{\partial n}{\partial \omega}} = \frac{c}{n_g \! \left( \omega \right)} $$

The wavenumber $ \small{\left( k \right)} $ is $ \tfrac{2 \pi}{\lambda} $ - this concept is sometimes also referred to a spectral phase. As multiple wavelengths of light transmit through a material, the longer wavelength (lower frequency) typically travels faster than shorter wavelengths (higher frequencies) because the group velocity is wavelength-dependent.² This results in a spectral spreading of the wavefront phase similar to the way light transmitting through a prism is dispersed into its component colors. Group velocity is defined as the first derivative of the phase velocity with respect to frequency, and the group velocity dispersion $ \small{\text{GVD}} $ is similarly defined as the derivative of the inverse group velocity with respect to frequency:

(6)$$ \text{GVD} = \frac{\partial}{\partial \omega} \left( \frac{1}{\nu _g} \right) = \frac{\partial}{\partial \omega} \left( \frac{\partial k}{ \partial \omega} \right) = \frac{\partial ^2 k}{\partial \omega ^2} $$

Group velocity is similar to spectral dispersion as they both correspond to the first derivative of refractive index with respect to wavelength or frequency. Likewise, $ \small{\text{GVD}} $ is similar to partial dispersion in that they are both second derivatives with respect to wavelength or frequency. Minimizing $ \small{\text{GVD}} $ in an optical design is similar to designing to minimize chromatic focal shift, except the designer will focus on group velocity and $ \small{\text{GVD}} $ rather than the Abbe number and partial dispersion.

A further discussion of $ \small{\text{GVD}} $ and its importance for ultrafast laser optics can be found in our Ultrafast Dispersion application note.