f/# (鏡頭光圈 / 光圈設定)

鏡頭上的f/#設定可控制多項鏡頭參數：總體光通量、景深以及於給定分辨率下產生對比度的能力。從根本上說，f/#是鏡頭的有效焦距(EFL)與有效孔徑(D_EP)之間的比率：

(1)$$ f/ \# = \frac{\text{EFL}}{D_{\text{EP}}}$$

大多數鏡頭的f/#都是透過轉動光圈調節環 (鏡頭的解剖結構)、進而打開和關閉內部的光圈來設定。標記光圈調節環的數字表示光通量及其關聯的孔徑。這些數字通常以√2的倍數增加。以√2為因數增加f/#會使光圈大小減半，有效地以2為因數來降低鏡頭的光通量。f/#更低的鏡頭被認為速度更快，而且允許更多光線通過系統，而f/#更高的鏡頭被認為速度更慢，並且光通量更少。表1顯示的範例為25mm焦距鏡頭的f/#、孔徑和有效孔徑。請注意，設定從f/1變為f/2，然後再從f/4變為f/8時，每個間隔的鏡頭孔徑會減半，有效面積也將以4為因數縮小。這裡描述了通量隨著鏡頭f/#增加而減少。

f/#	Lens Aperture Diameter (mm)	Aperture Opening Area (mm²)
1	25.0	490.8
1.4	17.9	251.6
2	12.5	122.7
2.8	8.9	62.2
4	6.3	31.2
5.6	4.5	15.9
8	3.1	7.5

表 1: 25mm單業鏡頭的f/#與有效面積之間的關係。隨著f/#增加，面積會減小，導致系統速度變慢，光通量也會減少。

f/#及其對鏡頭理論解析度、對比度和景深的影響

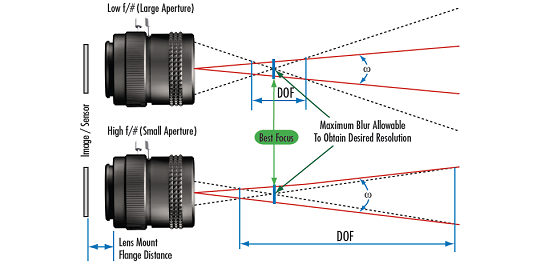
f/#的影響不僅限於光通量。具體來說，f/#與理論上的分辨率和對比以及景深(DOF)和鏡頭焦深直接相關 ( 有關景深(DOF) 的更多信息，請參閱景深和焦深)。此外，它還會影響特定鏡頭設計的像差。隨著像素大小繼續減小，f/#將成為限制系統效能的最重要因素之一，因為它與景深和解析度成反比。如表2所示，要求往往存在直接衝突，因此必須做出妥協。

f/#	Diffraction Limited Resolution	Depth of Field	Light Throughput	Numerical Aperture
	$Diffraction Limited Resolution Performance Changes$

表 2: 鏡頭效能隨f/#改變而變化。

f/#隨工作距離變更而變化

f/# 隨工作距離變化

公式1中的f/#是在放大倍率實際上為0的無限工作距離下定義的，從這種意義上來講，f/#的定義是受限的。通常在機器視覺應用中，相比無限遠的距離，物體要離鏡頭更近，並且公式2中將f/#_w更準確地表示為工作f/#。

(2)$$ \left( \text{f}/ \# \right)_w \approx \left( 1 + m \right) \times \left( \text{f}/ \# \right)$$

(2)

$$ \left( \text{f}/ \# \right)_w \approx \left( 1 + m \right) \times \left( \text{f}/ \# \right)$$

在計算工作f/#_w的公式中，m表示物鏡的近軸放大倍率（圖像與物體高度的比率）。請注意，m越接近0（物體越接近無限遠），工作f/#_w等於無限f/#。在工作距離較小的情況下，尤其要考慮工作f/#_w。例如，以-0.5X的放大倍率操作的f/2.8、25mm焦距鏡頭，有效工作f/#_w為f/4.2。這會影響成像品質以及鏡頭收光的能力。

f/#和數值孔徑(NA)

從鏡頭收光錐形角或數值孔徑(NA)的角度來探討總體光通量往往更加簡單。鏡頭的數值孔徑定義為像空間間中邊緣光線角的正弦（如圖1所示）。

Visual representation of f/#, both for a simple lens (a), and a real-world system (b).

圖 1: 針對簡單鏡頭(a)和實際系統(b)的f/#視覺再現。

務必記住，f/#和NA成反比。

(3)$$ \text{NA} = \frac{1}{2 \times \left( \text{f}/\# \right)}$$

(3)

$$ \text{NA} = \frac{1}{2 \times \left( \text{f}/\# \right)}$$

表3顯示了鏡頭的典型f/#佈局（後續每個數字都以√2為因數增加）及其與數值孔徑之間的關係。

f/#	1.4	2	2.8	4	5.6	8	11	16
NA	0.36	0.25	0.18	0.13	0.09	0.06	0.05	0.03

表 3: f/#與數值孔徑之間的關係。

採用數值孔徑標註而非f/#在顯微鏡中尤為常見，但務必記住的是，為顯微鏡物鏡所指定之數值孔徑值是於物體空間中指定，因為在這裡更容易收集光線。另一個有趣的類似情況是，無限共軛顯微鏡物鏡可以被認為是相反的機器視覺物鏡（於無限遠對焦）。調制轉換函數(MTF)和MTF曲線、解析度與對比度限制：艾里斑相關的部份介紹了關於f/#影響分辨率的更多資訊。傳感器相對照明、衰减以及暗角介紹了有關f/#和景深的詳細資訊。